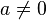Relações Métricas nos Polígonos Regulares

1- Polígono Inscrito

É inscrito quando os vértices são pontos da circunferência

2- Polígono Circunsecrito

É Circunscrito quando os lados sao tangentes a circunferência.

° Apótema de um polígono Regular

-> É um segmento de reta cuja extremidades é o centro da circunferência e o ponto médio ao lado do poligono.

-> É Sempre perpenticular ao lado.

Atividade complementar

Relação entre duas cordas concorrentes em uma circunferência.


1- Determine o valor de X

Atividade complementar

A Circunferência e Seus Elementos


1 - Determine o valor de X

Relação entre duas cordas concorrentes em uma circunferência

A Circunferência e Seus Elementos

 ° Reta Secante: Reta que corta a circunferência em dois pontos distintos

° Reta Tângente: Reta que corta a circunferência em um único ponto

* Ângulo Central *

O ângulo tem o mesmo valor do seu arco correspondente.

* Ângulo Inscrito *

A medida do ângulo inscrito é a metade da medida do seu arco correspondente.

*Arcos de uma circunferência*

Teorema de Pitágoras

Teorema de Pitágoras é o quadrado da hipotenusa igual a soma dos quadrados dos catetos (oposto e adjacente)


Formula: c²= a²+b²
onde C é a hipotenusa e A e B é os catetos.


exemplo:  
Calculando:
obs. H pode ser representado também por x.Vamos fazer assim então:


x²=12²+16²
x²=144+256
x²=400
x=√400
x=20 ou seja, o valor de h no triângulo é igual a 20.

Função Quadrática

A Função Quadrática também pode ser chamada de Função do 2º grau.

Forma:  ax²+b+c   onde 

- Algumas regrinhas que devemos saber:

1.O sinal do "a" é que define a posição da concavidade.

Se o 'a' for negativo a concavidade vai ser voltada para baixo:

exemplo: 

Se o 'a' for positivo a concavidade vai ser voltada para cima:

exemplo:   

2.Todo "c" (coeficiente) cota o eixo Y (ordenada)

3.A linha representada por X é chamada de abscissas e por Y é chamada de ordenada.

CALCULAR O ZERO DA FUNÇÃO

- forma de delta e baskara