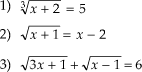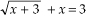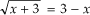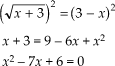Equações Incompletas: Resolução pela Fórmula de Bháskara

A resolução das equações incompletas na fórmula de Bháskara se resolve da mesma maneira, como se fosse uma equação completa(como vimos no post anterior),apenas mudamos o local da incógnita pelo seu valor,no caso se ela for incompleta 0.

Exemplo:

-4x²+20x=0                    (c=0)

∆ =(20)²-4 (-4) (0)

∆ =400+0 = 400

X= -20±√400  x'= -20+20= 0= 0    x''= -20-20= -40= 5

       2(-4)                 -8     -8                 -8       -8    -1 


Solução {0;5/-1}

Fórmula de Bháskara

Já vimos aqui no blog,anteriormente como identificar a,b e c em uma equação certo?! Então é agora que vamos usar isso:

a Fórmula de Bháskara(ou Fórmula Geral,como também pode ser chamada) tem a seguinte forma:

∆ = b² – 4 (a) (c)

Depois de calculá-lo usaremos essa outra forma aqui:

x = - b ± √∆ 
           2(a)

è É importante lembrar que para usar essa fórmula a equação deverá ser reduzida (e sempre será do 2º grau)

Exemplos:

(lembre-se que na equação sempre ela deve ser igualada a zero)

X²-8x+16=25

X²-8x+16-25=0 

X²-8x-9=0   (forma reduzida)

∆ =(-8)²-4 (1) (-9)

∆ =64+36 =  100

x = 8 ± √100   x=   8+10= 18 =9   x=8-10= -2 = -1
          2(1)              2         2                 2      2
        

Solução:{9,-1}

9x²+6x+1=0   (aqui ela já está na forma reduzida)

∆ = (6)²-4 (9) (1)

∆ = 36-36 = 0

X= -9±√0   x=-9-0= 9= 1  x=-9+0= 9= 1 

      2(9)           18    18  2        18    18   2

Solução:{1/2;1/2}

X²-8x+15=0

∆ =(-8)²-4 (1) (15)

∆ =64-60= 4

X= 8±√4  x= 8+2= 10= 5    x= 8-2= 6= 3

      2(1)          2       2                2     2

Solução:{5,3}

Equações Incompletas: Resolução reduzida

Vimos no post anterior que quando b ou c forem igual a 0 elas serão chamas de Equação Incompleta.

Exemplos:

x²-10=0      a=1 b=0 c= -10

4x²-6x=0   a=4 b= -6 c=0

3x²+5x=20   a=3 b=5 c=0                                                               

(importante: c (ou b) nunca serão o número que se encontra depois do = )

Resolução: nas equações incompletas teremos duas maneiras de resolução: a primeira pela fórmula de Bháskara e a outra pela forma reduzida. Vamos a essa então:

Quando b=0

X²-64=0

X²= ±64

X= ± √64

X=±8

Solução: {8,-8}

X²+25=0

X²= ±25

X= ± √25

X=±5

Solução: {5,-5}

X²-36=0

X²= ±36

X= ± √36

X=±6

Solução: {6,-6}

Quando c=0

X²-2x=0

X(x-2)=0

X=0   ou    x-2=0  / x=2  (-2 passa 2 para depois do igual)

Solução:{0,2}

X²-5x=0

X(x-5)=0

X=0   ou    x-5=0  / x=5

Solução:{0,5}

X²+8x=0

X(x+8)=0

X=0   ou    x+8=0  / x=-8  

Solução:{0,-8}

Identificando a, b e c de uma equação

-> Identificando a, b e c de uma equação

A:sempre será o número que estiver acompanhado de x²

B:sempre será o número que estiver acompanhado de x

C:sempre será o número que estiver sem nenhuma incógnita(ou seja,apenas o número)

Alguns Exemplos:

6x²-8x+9=0   a=6  b=-8  c=9

x²+5x-3=0     a=1  b=5  c=-3

5x²-x+8=0  a=5 b=-1 c=8

Observação:Em algumas equações pode existir b=0 e c=0 mas nunca A será 0.Quando b ou c forem igual a 0 elas serão chamas de Equação Incompleta.

(veremos isso no próximo post)

Segredo da Matemática e o Telefone

Faça seus amigos (as) ficarem de boca aberta descobrindo os telefonesdeles (as).

Como?É fácil. Quer aprender? Então peça para um amigo (a) seu, com uma calculadora em mãos para:

1º) Digitar os 4 primeiros números do telefone dele(a);

2º) Multiplicar por 80;

3º) Somar 1;

4º) Multiplicar por 250;

5º) Somar os 4 últimos números do telefone dele(a);

6º) Somar mais uma vez os 4 últimos números do telefone dele(a);

7º) Subtrair 250;

8º) Dividir 2.

O resultado será o telefone do seu amigo! Veja um exemplo:

Telefone 36633645

1º) 3663 x 80 = 293040

2º) 293040 + 1 = 293041

3º) 293041 x 250 = 73260250

4º) 73260250 + 3645 = 73263895

5º) 73263895 + 3645 = 73267540

6º) 73267540 - 250 = 73267290

7º) 73267290 / 2 = 36633645

Resultado: 36633645

Agora é so sair atras de alguem com uma calculadora na mão.. :)

Equações Biquadradas

Equação biquadrada é uma equação de quarto grau, que para achar os valores de suas raízes é preciso transformá-la em uma equação de 2º grau. 

Essa equação é escrita da seguinte forma geral: ax4 + bx2 + c = 0. 

Onde a ≠ 0.

Para encontrarmos as raízes, transformamos a equação do 4° grau ( biquadrada) a do 2° grau. Como?

Através da substituição de incógnitas.

Para entender melhor, preste atenção no exemplo abaixo.

4x4 – 17x2 + 4 = 0 → equação biquadrada 

 x² = y - Substitui

4y² - 17y + 4 = 0

∆ = (-17)² - 4 . 4 . 4

∆ = 289 - 64

∆ = 225

∆ = 15

Y=   17 +/- 15           

        _______   =  

             8

     

y' =  17 + 15

      ________   = 4

            8 

y'' = 17 - 15

     _________   = 1/4

           8              
                         

S { 4 ; 1  }

           4

Vejamos alguns exemplos:

Exemplo 1 :

x4 – 10x² + 9 = 0

   x² = y

y² - 10y + 9 = 0

∆ = (-16)² - 4 . 1 . 9

∆ = 100 – 36

∆ = 64

y= 10 +/- 8

           2

y’ = 18  =  9

        2

y’’ =    2   = 1

           2

S{ 9 ; 1}

Exemplo 2 :

X4 – 6x²  - 7 = 0

 X² = y

Y² - 6y – 7 = 0

∆ = (-6)² - 4 . 1 . 7

∆ = 36 + 28

∆ = 64

Y =  6+/- 8

           2

y’ =  14   = 7

         2

y’’=  - 2  = -  1

         2

S { 7 ; -1 }

Exemplo 3 :

3x4 – 10 x² = 0

x² = y

3y² - 10y = 0

∆ = (-10)²- 4 . 3 . 0

∆ = 100

Y = 10+/- 10   

           6

y’ = 10 + 10  =  20   = 10

           6             6        3

y’’ = 10-10  = 0   = 0

6                 6

S { 10  ; 0 }

       3


* IMPORTANTE lembrar que para o desenvolvimento das Equações Biquadradas, é necessário saber calcular Equações do 1° e 2° grau, Formula de Bhaskara, delta, fatoração, radiciação, etc.

* Equação Irracional *

Equação Irracional é uma equação em que há incógnita em um ou mais radicais. São equações irracionais:

















p.S: As raízes podem ter qualquer índice.


Há 4 passos que facilitam na resolução da Equação Irracional


1° Passo:  Isolar o radical em um dos membros
2° Passo:  Elevar os dois membros, dependo do índice do Radical.
3° Passo:  Calcular uma equação do 1° grau ou 2° grau
4° Passo:  Verificar se a raiz encontrada é verdadeira


Vejamos um exemplo:


Equação a ser resolvida:


1° Passo: Isolar o radical em um dos membros







2° Passo: Elevar os dois membros, dependendo do índice do radical.













3° Passo: Calcular uma equação do 1° ou 2° Grau. ( Quando for equação do 2° grau, se calcula o Delta e o Bhaskara)

4° Passo: Verificar se a raiz encontrada é verdadeira

Notamos que 1 é solução da equação mas 6 não é, assim sendo:

S={1}

Exemplo 1

√x+2 - 3= 1

√x+2  = 4

(√x+2)² = (4)²

x+2 = 16

x = 14

Verificação:

√14+2 – 3 = 1

√14+2 = 4

(√14+2)² = (4)²

14+2 = 16

16 = 16   V

S = { 14 }

Exemplo 2

√x+6 = √9

(√x+6)² = (√9)²

x+6 = 9

x = 9 - 6

x = 3

Verificação

√3+6 = √9

(√3+6)² = (√9)²

3+6= 9

 9 = 9

S= {3}

Exemplo 3

√√x+2 = 2

(√√x+2)² = (2)²

√x+2 = 4

(√x+2)² = (4)²

x+2 = 16

x = 14

Verificação

√√14+2 = 2

(√√14+2)² = (2)²

√14+2 = 4

(√14+2)² = (4)²

14 + 2 = 16

16 = 16

S: {14}