quarta-feira, 30 de junho de 2010
P.s
Por enquanto ficaremos por aqui. Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e gostaria de cooperar com dicas, indicar algum blog legal de matemática, programas legais que conhece, artigos, trabalhos de escola. Mande um e-mail lorenaa@atarde.com.br ,ou comente aqui mesmo. Agradeço sua cooperação, comentários, dicas, críticas e sugestões.
A Matemática e a Poesia
Um Quociente apaixonou-se Um dia, Doidamente, Por uma Incógnita. Olhou-a com seu olhar inumerável E viu-a, do Ápice à Base... Uma Figura Ímpar; Olhos rombóides, boca trapezóide, Corpo ortogonal, seios esferóides. Fez da sua uma vida Paralela à dela. Até que se encontraram No Infinito. "Quem és tu?" indagou ele Com ânsia radical. "Sou a soma do quadrado dos catetos. Mas pode chamar-me Hipotenusa." E ao falarem descobriram que eram O que, em aritmética, corresponde A almas irmãs: Primos-entre-si. E assim se amaram Ao quadrado da velocidade da luz. Numa sexta potenciação Traçando Ao sabor do momento E da paixão Rectas, curvas, círculos e linhas sinusoidais. Escandalizaram os ortodoxos das fórmulas euclidianas E os exegetas do Universo Finito. Romperam convenções newtonianas e pitagóricas. E, enfim, resolveram casar, Constituir um lar. Millôr Fernandes | Mais do que um lar. Uma Perpendicular. Convidaram para padrinhos O Poliedro e a Bissectriz. E fizeram planos, equações e diagramas para o futuro Sonhando com uma felicidade Integral E diferencial. E casaram-se e tiveram uma secante e três cones Muito engraçadinhos. E foram felizes Até aquele dia Em que tudo, afinal, Vira monotonia. Foi então que surgiu O Máximo Divisor Comum... Freqüentador de Círculos Concêntricos. Viciosos. Ofereceu-lhe, a ela, Uma Grandeza Absoluta, E reduziu-a a um Denominador Comum. Ele, Quociente, percebeu Que com ela não formava mais Um Todo. Uma Unidade. Era o Triângulo, Tão chamado amoroso. Desse problema ela era a fração Mais ordinária. Mas foi então que Einstein descobriu A Relatividade. E tudo o que era espúrio passou a ser Moralidade. Como, aliás, em qualquer Sociedade. |
Despreparados
Despreparados
Este poderia ser mais um título de um filme de sucesso. Despreparados ou até desesperados, sei lá. E sem final feliz, mas é uma das milhares de pérolas da matemática,ou melhor uma pérola negra. Agora eu pergunto o que foi que aconteceu com este cara, se assustou com a questão, se desesperou?E pior que isto é muito comum numa prova de matemática. Alguns chegam ao extremo de ½ hora antes da prova, irem pesquisar no yahoo respostas, google; pra ver se alguém sabe algo relacionado ao conteúdo da prova que ira fazer;digo isto porque eu já respondi para alguns destes gênios.
Pô, deixar para fazer pesquisas sobre o conteúdo de matemática no dia da prova, só pode dar nisso que vocês vêem na figura, e pior ainda pedem um programinha que faça todas as questões, enquanto ele navega pelo orkut; essa e de lascar.
Bom, então vou dar umas dicas, que não são novas, é do tempo da minha vó,logo todos já deveriam saber.
Em primeiro lugar, tem que estar descansado,sem sono,sem ninguém na volta te distraindo;tem alguns que conseguem estudar com som, televisão, conversando, etc.
Mas nem todos são tão concentrados assim, eu mesmo sou um pouco aéreo, por isso gosto de estudar sozinha.
Em segundo muita prática, exercícios,anotar as dúvidas,perguntar para colegas, mais adiantados,não tem que ficar com vergonha não,tá com dificuldades?então tem que perguntar pô.o professor esta dentro da aula é pra auxiliar o aluno;passar matéria qualquer um faz.
Estudar em grupo de três ou quatro pessoas é uma boa pedida, mas não exagere doze ou treze pessoas, bebida, som, quarto,namorada(o), isso não vai dar certo; e por ai vai.
Conseguir uns programas, que auxiliem no desenvolvimento do exercício,ajuda a descobrir a resposta dai fica mais fácil,com a resposta em mãos é só treinar bastante.
mas não vai adiantar se usar programas para conseguir respostas e não estudar,ai vai ficar no mesmo,tem que treinar.
Pra finalizar vê se deixa a preguiça de lado e estuda todos os dias, não deixa pra ultima hora, senão acontece a mesma coisa que o nosso amigo da figura.
Estuuuuuuuuda meniiiino(a).
Oração Para a Prova de Matemática
Para o aluno que nunca perde a fé, mesmo naquelas horas difíceis, - quase impossíveis- acredita que uma oração antes da prova de matemática pode ajudar, vou deixar duas bem legais que encontrei no site do thiago, e que têm tudo a ver com a nossa disciplina.
" Mestre matemático que estais na sala,
Santificada seja a Vossa prova,
Seja de Álgebra ou de Geometria,
O zero de cada dia não nos dai hoje,
Perdoai as nossas bagunças,
Assim como perdoamos os Vossos Teoremas,
Não nos deixeis cair em recuperação,
Mas nos livrai da reprovação,
Amém."
Esta é para quem está desesperado!
" Ave matemático cheio de malícias,
O temor esteja convosco,
Bendita seja a prova de vossa cabeça,
Socorro !!!
Santa cola, mãe do aluno,
Rogai por nós agora
E no choro da má sorte,
Amém."
Autores : jarbas,josiane,thiago.
Equação Fracionária Redutível
-as equações fracionárias redutíveis são todas aquelas que em seu denominador é apresentado uma variável.
exemplo:
- Precisamos excluir do conjunto os valores da incognita para que anulem os denominadores da equação.Para isso denominador não pode ser 0 pois não existe divisão por zero.
exemplo:
3 = 4T = 3(3T+1) = 8T² _
2T 3T+1 2T(3T+1) 2T(3T+1)
- a maneira de se descobrir o denominador de duas frações é multiplicar um pelo outro.Para isso nesse exemplo,usamos um método mais fácil,repetir os dois para depois resolve-lo.
Método Prático:
- Calcular o MMC
- Eliminar os denominadores
- Reduzir a equção
Marcadores:
Equação fracionaria redutivel
Produto das Raízes
é resolvido da mesma maneira da soma das raízes,a diferença é que agora temos uma multiplicação no lugar da soma (:
Multiplica-se as raízes: x' . x''
-b-√∆ . -b+√∆ = (-b)²-(√∆)² = b²-(b²-4ac)=
2a 2a 4a² 4a²
2a 2a 4a² 4a²
b²-b²+4ac = 4ac = {divide a fração por 4a } = c
4a² 4a² a’
{a²:a=a / divisão subtrai os expoentes}
{a²:a=a / divisão subtrai os expoentes}
Marcadores:
Produto das Raizes
Soma das Raízes
soma-se as raízes: x’ + x”
-b-√∆ + -b+√∆ = -b-√∆-b+√∆
2a 2a 2a
2a 2a 2a
-> soma as duas facões
-> cancelam os termos opostos (ou seja,termos iguais mais com sinais
diferentes) exemplo na equação: -√∆ e +√∆
| -b-b= -2b | √∆ foram cancelados pois são postos | mantem-se o denominador.
Que fica assim:
-2b = -b ->-2 e 2 são divisíveis,então dividem e se da o resultado 2a a
Marcadores:
Soma das Raizes
terça-feira, 29 de junho de 2010
Equações Incompletas: Resolução pela Fórmula de Bháskara
A resolução das equações incompletas na fórmula de Bháskara se resolve da mesma maneira, como se fosse uma equação completa(como vimos no post anterior),apenas mudamos o local da incógnita pelo seu valor,no caso se ela for incompleta 0.
Exemplo:
-4x²+20x=0 (c=0)
∆ =(20)²-4 (-4) (0)
∆ =400+0 = 400
X= -20±√400 x'= -20+20= 0= 0 x''= -20-20= -40= 5
2(-4) -8 -8 -8 -8 -1
Solução {0;5/-1}
Solução {0;5/-1}
Marcadores:
Equação incompleta
Fórmula de Bháskara
Já vimos aqui no blog,anteriormente como identificar a,b e c em uma equação certo?! Então é agora que vamos usar isso:
a Fórmula de Bháskara(ou Fórmula Geral,como também pode ser chamada) tem a seguinte forma:
∆ = b2 – 4 (a) (c)
Depois de calculá-lo usaremos essa outra forma aqui:
x = - b ± √∆
2(a)
2(a)
è É importante lembrar que para usar essa fórmula a equação deverá ser reduzida (e sempre será do 2º grau)
Exemplos:
(lembre-se que na equação sempre ela deve ser igualada a zero)
X²-8x+16=25
X²-8x+16-25=0
X²-8x-9=0 (forma reduzida)
∆ =(-8)²-4 (1) (-9)
∆ =64+36 = 100
x = 8 ± √100 x= 8+10= 18 =9 x=8-10= -2 = -1
2(1) 2 2 2 2
2(1) 2 2 2 2
Solução:{9,-1}
9x²+6x+1=0 (aqui ela já está na forma reduzida)
∆ = (6)²-4 (9) (1)
∆ = 36-36 = 0
X= -9±√0 x=-9-0= 9= 1 x=-9+0= 9= 1
2(9) 18 18 2 18 18 2
Solução:{1/2;1/2}
X²-8x+15=0
∆ =(-8)²-4 (1) (15)
∆ =64-60= 4
X= 8±√4 x= 8+2= 10= 5 x= 8-2= 6= 3
2(1) 2 2 2 2
Solução:{5,3}
Equações Incompletas: Resolução reduzida
Vimos no post anterior que quando b ou c forem igual a 0 elas serão chamas de Equação Incompleta.
Exemplos:
x²-10=0 a=1 b=0 c= -10
4x²-6x=0 a=4 b= -6 c=0
3x²+5x=20 a=3 b=5 c=0
(importante: c (ou b) nunca serão o número que se encontra depois do = )
Resolução: nas equações incompletas teremos duas maneiras de resolução: a primeira pela fórmula de Bháskara e a outra pela forma reduzida. Vamos a essa então:
Quando b=0
X²-64=0
X²= ±64
X= ± √64
X=±8
Solução: {8,-8}
X²+25=0
X²= ±25
X= ± √25
X=±5
Solução: {5,-5}
X²-36=0
X²= ±36
X= ± √36
X=±6
Solução: {6,-6}
Quando c=0
X²-2x=0
X(x-2)=0
X=0 ou x-2=0 / x=2 (-2 passa 2 para depois do igual)
Solução:{0,2}
X²-5x=0
X(x-5)=0
X=0 ou x-5=0 / x=5
X²+8x=0
X(x+8)=0
X=0 ou x+8=0 / x=-8
Solução:{0,-8}
Marcadores:
Equação incompleta
Identificando a, b e c de uma equação
-> Identificando a, b e c de uma equação
A:sempre será o número que estiver acompanhado de x²
B:sempre será o número que estiver acompanhado de x
C:sempre será o número que estiver sem nenhuma incógnita(ou seja,apenas o número)
Alguns Exemplos:
6x²-8x+9=0 a=6 b=-8 c=9
x²+5x-3=0 a=1 b=5 c=-3
5x²-x+8=0 a=5 b=-1 c=8
Observação:Em algumas equações pode existir b=0 e c=0 mas nunca A será 0.Quando b ou c forem igual a 0 elas serão chamas de Equação Incompleta.
(veremos isso no próximo post)
Marcadores:
Equação incompleta
segunda-feira, 28 de junho de 2010
Segredo da Matemática e o Telefone
Faça seus amigos (as) ficarem de boca aberta descobrindo os telefonesdeles (as).
Como?É fácil. Quer aprender? Então peça para um amigo (a) seu, com uma calculadora em mãos para:
2º) Multiplicar por 80;
3º) Somar 1;
4º) Multiplicar por 250;
5º) Somar os 4 últimos números do telefone dele(a);
6º) Somar mais uma vez os 4 últimos números do telefone dele(a);
7º) Subtrair 250;
8º) Dividir 2.
Telefone 36633645
1º) 3663 x 80 = 293040
2º) 293040 + 1 = 293041
3º) 293041 x 250 = 73260250
4º) 73260250 + 3645 = 73263895
5º) 73263895 + 3645 = 73267540
6º) 73267540 - 250 = 73267290
7º) 73267290 / 2 = 36633645
Agora é so sair atras de alguem com uma calculadora na mão.. :)
sábado, 19 de junho de 2010
Equações Biquadradas
Equação biquadrada é uma equação de quarto grau, que para achar os valores de suas raízes é preciso transformá-la em uma equação de 2º grau.
Essa equação é escrita da seguinte forma geral: ax4 + bx2 + c = 0.
Onde a ≠ 0.
Para encontrarmos as raízes, transformamos a equação do 4° grau ( biquadrada) a do 2° grau. Como?
Através da substituição de incógnitas.
Para entender melhor, preste atenção no exemplo abaixo.
4x4 – 17x2 + 4 = 0 → equação biquadrada
x² = y - Substitui
4y² - 17y + 4 = 0
∆ = (-17)² - 4 . 4 . 4
∆ = 289 - 64
∆ = 225
∆ = 15
Y= 17 +/- 15
_______ =
8
y' = 17 + 15
________ = 4
8
y'' = 17 - 15
_________ = 1/4
8
S { 4 ; 1 }
4
Vejamos alguns exemplos:
Exemplo 1 :
x4 – 10x² + 9 = 0
x² = y
y² - 10y + 9 = 0
∆ = (-16)² - 4 . 1 . 9
∆ = 100 – 36
∆ = 64
y= 10 +/- 8
2
y’ = 18 = 9
2
y’’ = 2 = 1
2
S{ 9 ; 1}
Exemplo 2 :
X4 – 6x² - 7 = 0
X² = y
Y² - 6y – 7 = 0
∆ = (-6)² - 4 . 1 . 7
∆ = 36 + 28
∆ = 64
Y = 6+/- 8
2
y’ = 14 = 7
2
y’’= - 2 = - 1
2
S { 7 ; -1 }
Exemplo 3 :
3x4 – 10 x² = 0
x² = y
3y² - 10y = 0
∆ = (-10)²- 4 . 3 . 0
∆ = 100
Y = 10+/- 10
6
y’ = 10 + 10 = 20 = 10
6 6 3
y’’ = 10-10 = 0 = 0
6 6
S { 10 ; 0 }
3
* IMPORTANTE lembrar que para o desenvolvimento das Equações Biquadradas, é necessário saber calcular Equações do 1° e 2° grau, Formula de Bhaskara, delta, fatoração, radiciação, etc.
* IMPORTANTE lembrar que para o desenvolvimento das Equações Biquadradas, é necessário saber calcular Equações do 1° e 2° grau, Formula de Bhaskara, delta, fatoração, radiciação, etc.
Marcadores:
Equação Biquadrada
domingo, 13 de junho de 2010
* Equação Irracional *
Equação Irracional é uma equação em que há incógnita em um ou mais radicais. São equações irracionais:
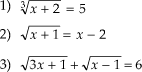
p.S: As raízes podem ter qualquer índice.
Há 4 passos que facilitam na resolução da Equação Irracional
1° Passo: Isolar o radical em um dos membros
2° Passo: Elevar os dois membros, dependo do índice do Radical.
3° Passo: Calcular uma equação do 1° grau ou 2° grau
4° Passo: Verificar se a raiz encontrada é verdadeira
Vejamos um exemplo:
Equação a ser resolvida:
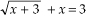
1° Passo: Isolar o radical em um dos membros
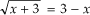
2° Passo: Elevar os dois membros, dependendo do índice do radical.
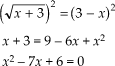
3° Passo: Calcular uma equação do 1° ou 2° Grau. ( Quando for equação do 2° grau, se calcula o Delta e o Bhaskara)
4° Passo: Verificar se a raiz encontrada é verdadeira
Notamos que 1 é solução da equação mas 6 não é, assim sendo:
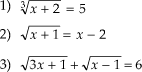
p.S: As raízes podem ter qualquer índice.
Há 4 passos que facilitam na resolução da Equação Irracional
1° Passo: Isolar o radical em um dos membros
2° Passo: Elevar os dois membros, dependo do índice do Radical.
3° Passo: Calcular uma equação do 1° grau ou 2° grau
4° Passo: Verificar se a raiz encontrada é verdadeira
Vejamos um exemplo:
Equação a ser resolvida:
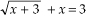
1° Passo: Isolar o radical em um dos membros
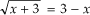
2° Passo: Elevar os dois membros, dependendo do índice do radical.
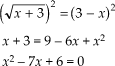
3° Passo: Calcular uma equação do 1° ou 2° Grau. ( Quando for equação do 2° grau, se calcula o Delta e o Bhaskara)
4° Passo: Verificar se a raiz encontrada é verdadeira
Notamos que 1 é solução da equação mas 6 não é, assim sendo:
S={1}
Exemplo 1
√x+2 - 3= 1
√x+2 = 4
(√x+2)² = (4)²
x+2 = 16
x = 14
Verificação:
√14+2 – 3 = 1
√14+2 = 4
(√14+2)² = (4)²
14+2 = 16
16 = 16 V
S = { 14 }
Exemplo 2
√x+6 = √9
(√x+6)² = (√9)²
x+6 = 9
x = 9 - 6
x = 3
Verificação
√3+6 = √9
(√3+6)² = (√9)²
3+6= 9
9 = 9
S= {3}
Exemplo 3
√√x+2 = 2
(√√x+2)² = (2)²
√x+2 = 4
(√x+2)² = (4)²
x+2 = 16
x = 14
Verificação
√√14+2 = 2
(√√14+2)² = (2)²
√14+2 = 4
(√14+2)² = (4)²
14 + 2 = 16
16 = 16
S: {14}
Marcadores:
Equação Irracional
Assinar:
Comentários (Atom)



